how to find the range of a parabola

Quadratic Function

The general form of a quadratic function is $f (x) = a x^{2} + b x + c$ . The graph of a quadratic function is a parabola , a type of $2$ -dimensional curve.

The "basic" parabola, $y = x^{2}$ , looks like this:

The function of the coefficient $a$ in the general equation is to make the parabola "wider" or "skinnier", or to turn it upside down (if negative):

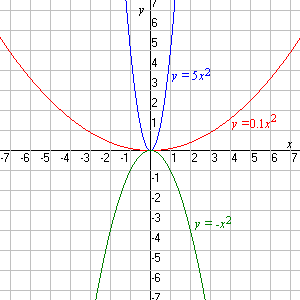
If the coefficient of $x^{2}$ is positive, the parabola opens up; otherwise it opens down.

The Vertex

The vertex of a parabola is the point at the bottom of the " $U$ " shape (or the top, if the parabola opens downward).

The equation for a parabola can also be written in "vertex form":

$y = a {(x - h)}^{2} + k$

In this equation, the vertex of the parabola is the point $(h, k)$ .

You can see how this relates to the standard equation by multiplying it out:

$y = a (x - h) (x - h) + k$

$y = a x^{2} - 2 a h x + a h^{2} + k$

The coefficient of $x$ here is $- 2 a h$ . This means that in the standard form, $y = a x^{2} + b x + c$ , the expression

$- \frac{b}{2 a}$

gives the $x$ -coordinate of the vertex.

Example:

Find the vertex of the parabola.

$y = 3 x^{2} + 12 x - 12$

Here, $a = 3$ and $b = 12$ . So, the $x$ -coordinate of the vertex is:

$- \frac{12}{2 (3)} = - 2$

Substituting in the original equation to get the $y$ -coordinate, we get:

$y = 3 {(- 2)}^{2} + 12 (- 2) - 12$

$= - 24$

So, the vertex of the parabola is at $(- 2, - 24)$ .

The Axis of Symmetry

The axis of symmetry of a parabola is the vertical line through the vertex. For a parabola in standard form, $y = a x^{2} + b x + c$ , the axis of symmetry has the equation

$x = - \frac{b}{2 a}$

Note that $- \frac{b}{2 a}$ is also the $x$ -coordinate of the vertex of the parabola.

Example:

Find the axis of symmetry.

$y = 2 x^{2} + x - 1$

Here, $a = 2 and b = 1$ . So, the axis of symmetry is the vertical line

$x = - \frac{1}{4}$

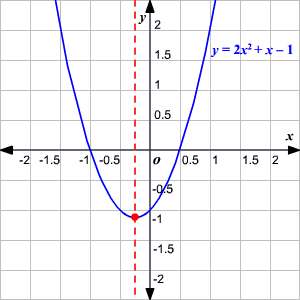
Intercepts

You can find the $y$ -intercept of a parabola simply by entering $0$ for $x$ . If the equation is in standard form, then you can just take $c$ as the $y$ -intercept. For instance, in the above example:

$y = 2 {(0)}^{2} + (0) - 1 = - 1$

So the $y$ -intercept is $- 1$ .

The $x$ -intercepts are a bit trickier. You can use factoring , or completing the square , or the quadratic formula to find these (if they exist!).

Domain and Range

As with any function, the domain of a quadratic function $f (x)$ is the set of $x$ -values for which the function is defined, and the range is the set of all the output values (values of $f$ ).

Quadratic functions generally have the whole real line as their domain: any $x$ is a legitimate input. The range is restricted to those points greater than or equal to the $y$ -coordinate of the vertex (or less than or equal to, depending on whether the parabola opens up or down).